The Heat Transfer Equation’s Constant ‘C’, Explained
In the HVAC industry, engineers will use the following equation1 to determine the amount of sensible heat transfer taking place when introducing airflow into any process or space. The equation is:
Q = C x cfm x dT, where
- Q is the amount of sensible heat transferred (lost or gained by the air), with units of Btu per hour (i.e. Btu/hr);
- C is a constant, usually 1.08, with units of Btu min / ft3 hr F;
- cfm is the amount of air being moved or transferred in the process, in cubic ft per minute (i.e. ft3/min);
- dT is the difference in temperature of the air during the process, whether it gains heat or loses heat; in units of degree Fahrenheit (F).
This equation is used to evaluate how much heat is gained or lost by a quantity of air that is introduced into a space or process. In comfort cooling situations (i.e., our typical room AC conditioned application), cold air is introduced into a space and done to absorb heat and moisture from the space; thereby maintaining the space at a predetermined comfortable temperature and moisture level.
In essence, heat entering the space (through the envelope, adjacent spaces, or from sources inside) is transferred to the air… and the space is kept at a desired lower temperature and relative humidity. Conversely, heated air can be used to transfer heat into another medium.
The Values of the Numerical Constant C
Turning our attention to C, it is equal to 1.08 for typical heat transfer airflow problems encountered in everyday applications, such as comfort cooling for instance. The three factors that make up the constant C are:
The density of the air (ρ), the specific heat capacity of air (cp) and a conversion factor to convert 60 minutes to hours. The units for each of the factors are:
• density, (ρ) = lbs per cubic foot of air (i.e. lbs/ft3);
• specific heat capacity of air, (cp ) = 0.24 Btu per lb of air F (i.e. Btu / lb F);
• 60 minutes per hour (i.e. 60 min / hr);
Explicitly then, C = density x specific heat capacity of air x 60... or symbolically, C = ρ x cp x 60.
Re Specific Heat Capacity
In laymen’s terms, this parameter represents the amount of heat required to raise the temperature of a unit mass of a material by one degree F. The specific heat capacity of air is taken to be 0.24 for most processes we encounter. This value is reliably used for a range of conditions that envelope between about -150 deg F and 200 deg F, and are at constant pressure associated with sea level elevation. In essence then, a pound of air, at sea level, at a temperature of say, 80 deg F, will need to absorb “x” amount of BTUs, in this case 0.24 BTUs [to raise the temperature of the pound of air by one degree F].
This value is stable so long as the air is within the temperature range mentioned, and at constant pressure. But beyond this temperature and pressure range, the value changes.
Back to our discussion... In comfort cooling applications, where the airflow is introduced into a space typically at 55 or 56 degrees, and about 95% relative humidity (RH), and returned back to the air handler at 75 degrees and about 50% RH, the value of C is usually 1.08. Let’s look at why.
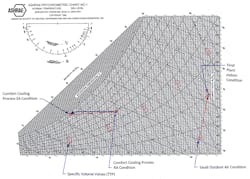
Above, Figure 1 shows a psychrometric chart for air at conditions of sea level pressure and temperatures between 35 F and 120 F. On it, just left of center, is a process path representing the process of cooling the air, from the point of it entering the air handler (as return air) to the point of discharge from the cooling coil (as cold supply air reaches about 95% RH), and back again to the air handler (at 75 F and 50% RH).
The density of air in the range encountered in this area varies between 0.073 lbs/ft3 to 0.076 lbs/ft3. The density is calculated from finding the inverse of the specific volume of the air at the two state points we are discussing; the specific volume is directly found on the psychrometric charts. At the supply condition of 55 F / 95% RH the specific volume is approximately 13.15 ft3/lb (the corresponding density = 0.076 lbs/ft3) and the specific volume of the return air at 75 F / 50% RH is approximately 13.67 ft3/lb (density = 0.073 lbs/ft3). Therefore, the average density of the air during this process is nearly 0.075 lbs/ft3. This is the value used in C.
Thus, C = ρ x cp x 60 = 0.075 x 0.24 x 60 = 1.08 Btu min/ hr ft3 F.
So, the value of C can be set at 1.08 for those types of air conditioned processes needed for comfort cooling applications. However, there are other situations where the value of C would need to change, depending on the process or specific application.
Let’s investigate two other such situations: One in cold Alaska and the other in hot Saudi Arabia. In Anchorage, AK, let’s say a laboratory wants to bring in cold outside air to cool another medium via a heat exchanger.
Cold Alaska
The laboratory’s process is to cool 150-degree process water down to 120 degrees for general plant use. Let’s say we need 30 gpm of water continuously. The water will be cooled by the incoming outside air, then the outside air continues on to another process [where it may pick up more heat, cooling another medium in yet another process]. During the first heat transfer phase, the increase in temperature of the OA is selected as 40 degrees F.
Thus, the heat required to be transferred from the water is: Q = 500 x gpm x dT. Substituting values, we have: Q = 500 x 30 gpm x 30 F = 450,000 Btu/hr.
For Anchorage, the 99.6% OA DB temperature is -8.7 F2. But let’s use -9.0 F, and assume about 20% RH. That’s very, very, dry air.
The amount of OA cfm at -9.0 F needed to cool down the water is:
450,000 Btu/hr = C x cfm x dT. We will need to find C here before we can solve for cfm airflow.
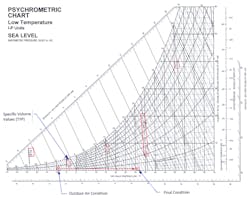
Above, in Figure 2, a psychrometric chart for low temperature applications at sea level, we see the specific volume of air at -9.0 F and 20% RH is about 11.38 ft3/lb. The corresponding density is 0.0878 lbs/ft3. At the end of the process, when the OA has increased by 40 degrees F and reached 31 degrees F, the specific volume has increased to about 12.38 ft3/lb. The corresponding density is 0.0808 lb/ft3. Thus, the average value of density during this process here is exactly 0.0843 lb/ft3. Let’s use this value in the following computation to find C.
Recall that C is equal to the specific heat of air x 60 x density, or... C = 0.24 x 60 x 0.0843 = 1.21 Btu min/hr ft3 F. Note that the value of C increased. This is due to colder air being denser, and thus heavier, per unit of volume.
Solving for the airflow required to cool the process water, we get: (450,000 ÷ (1.21 x 40)) = 9,297 cfm.
That’s a phenomenal amount of cold OA to be bringing into a building, but I am making a point here about the need to be precise using the correct value of C based on actual conditions. Using a value of C = 1.08 here would have yielded 10,416 cfm, an erroneous 12% increase in air. Your fan motor hp and motor’s electrical feed would have been oversized unnecessarily.
By the way, the fan should be sized for the condition of the outside air before being heated, as that is the condition where the air is both most dense and heaviest.
A Hot and Dry Situation
Similarly, on the opposite end of the temperature scale, let’s refer to Figure 1 again for a different situation. this time in Riyadh, Saudi Arabia. There, we are dealing with hot and dry ambient air.
We want to bring in very hot dry summer air to mitigate a water treatment plant’s indoor condition that is overly humid and hotter. The relatively cooler but dry outdoor air will be introduced into the plant directly to pick up moisture and heat inside the plant’s indoor space (on a once-through configuration).
We’ll use the 1% cooling dry bulb and mean coincident wet bulb temps from ASHRAE3; thus 111.1 DB / 66.1 MCWB are the conditions. Let’s round these to 111 F and 66 F. Without the outdoor air for cooling and moisture control, the indoor environment would be much hotter and wetter than when ventilated with OA.
The same amount of air will be exhausted at another location of the plant, so the process is once-through with 100% OA. With OA ventilation the plant’s desired indoor condition is 115 deg F and 20% RH. The final state point of the OA will be the same as the indoor condition noted. Note that the OA is heated by 4 deg F as it picks up internal plant heat.
So, looking at Figure 1 again, you’ll see the process over to the right of the chart. The OA condition is noted, as is the final plant indoor condition. See that the OA has picked up moisture and a little heat, as the process takes the air on a path up to the right.
Let’s assume the ventilation air is required to absorb 40,000 Btu/hr of heat inside the plant in order to bring the temperature down to 115 deg F. Let’s now find how much airflow is required to achieve this.
Again our heat transfer equation is: Q = C x cfm x dT, where
Q = 40,000 Btu/hr
cfm = ?
dT = 4 F
Now, let’s calculate the value of C for this scenario...
Initial OA condition = 111 F DB and 66 F WB. Its specific volume is approximately 14.47 ft3/lb. Its density is the inverse, or 1/14.47 = 0.0691 lbs/ft3.
Final plant indoor condition = 115 F and 20% RH. The specific volume is approximately 14.78 ft3/lb. The density equals 0.0676 lbs/ft3.
The average density for the process thus = 0.0683 lbs/ft3 . However, let’s round to 0.068.
Therefore, C = 0.24 x 0.068 x 60 = 0.9792, or 0.98.
Solving for the airflow needed to cool the plant: (40,000 ÷ (0.98 x 4)) = 10,204 cfm.
Had we used C = 1.08 here, the amount of cfm would have been less than that calculated, and the plant would have been a bit hotter and wetter than intended.
Thus, we’ve seen three situations where our constant C, used in our heat transfer equation, is not so constant after all, but actually changes. The greatest changes occur at the extremes, away from our familiar air conditioning (comfort cooling) application. However, in industrial settings where large energy processes require greater amounts of energy exchange, heat transfer, and involve temperature extremes, more accuracy is required when completing your calculations.
Conclusion
In engineering, accuracy is vitally important. Without it, liabilities increase. Issues such as oversizing or undersizing of equipment (in this case a fan moving OA) will result in extra costs and/or performance concerns. At an extreme, faulty engineering can even result in injury and death. Though the value of an equation’s constant in this case is not life-threatening, it can alter the performance of a fan system to a point of degraded and costly performance. So, be accurate in the work that is done and strive for doing the engineering correctly the first time.
References
1. 2017 ASHRAE Fundamentals, Chapter 16, “Ventilation and Infiltration”, Equation #33;
2. Temperature at Anchorage’s International Airport - ASHRAE 2017 Fundamentals, Chapter 14, “Climatic Design Information”;
3. Temperature at Riyadh King Salman AB (Air Base), 2017 ASHRAE Fundamentals, Chapter 14, “Climatic Design Information”.