New Method for Calculating Evaporation From Occupied Swimming Pools
Evaporation from swimming pools increases with the number of occupants and the intensity of their activity. Removing evaporated moisture so humidity does not exceed safe limits is the role of ventilation/dehumidification systems. Design equipment capacity has to match the evaporation that occurs at maximum occupancy. Pools, however, seldom see maximum occupancy and indeed are unoccupied much of the time. For accurate determination of energy consumption and the design of effective control strategies, the rate of evaporation at partial occupancy needs to be calculated.
Many formulas for calculating evaporation from occupied pools have been published. ASHRAE1 gives a formula for occupied pools, but does not give the effect of variations in number of occupants or state the occupancy density to which the formula applies. Similar is the situation with the VDI formula.2 Smith, Jones, and Lof3 and Hens4 have presented formulas based on their own test data, which include the effect of number of occupants, but those formulas have not been verified with other data. In 2003, this author introduced two formulas, one empirical and one theoretical.5 While those formulas showed reasonable agreement with data from several sources, it was felt greater accuracy was needed. The author’s efforts to meet that need have resulted in a new formula showing good agreement with all available test data. This article presents the new formula, as well as lookup tables to simplify its use.
New Formula for Occupied Pools
The following new formula was developed through analysis of test data:
E ÷ E0 = 1.9 − 336 (Dr − Dw) + 57 (N ÷ A) (1)
where:
E = evaporation from occupied pool, pounds per hour per square foot
E0 = evaporation from unoccupied pool, pounds per hour per square foot
Dr = density of air at room temperature and humidity, pounds per cubic foot
Dw = density of air saturated at water-surface temperature, pounds per cubic foot
N = number of people in pool
A = area of pool’s water surface, square feet
Equation 1 applies to numbers of people per square foot of water surface (N ÷ A) greater than or equal to 0.0046. When a pool is unoccupied, evaporation (E ÷ E0) equals 1. For numbers of people per square foot of water surface less than 0.0046, interpolate between evaporation at 0.0046 people per square foot of water surface and 1.
Unoccupied-pool evaporation rate (E0) is calculated using the author’s published method.6,7 According to the method, evaporation rate is the larger of the rates given by the following equations:
E0 = 290 Dw (Dr − Dw)1/3 (Ww − Wr) (2)
E0 = 0.125 (pw − pr) (3)
where:
Ww = humidity ratio of air saturated at water-surface temperature, pounds of moisture per pound of air
Wr = humidity ratio of air at room temperature and humidity, pounds of moisture per pound of air
pw = vapor pressure of moisture in air saturated at water-surface temperature, inches of mercury
pr = vapor pressure of moisture in air at room temperature and humidity, inches of mercury
To simplify use of these formulas, tables 1 and 2 were prepared. Table 1 gives evaporation rate from an unoccupied pool at typical swimming-pool air and water conditions according to equations 2 and 3. Table 2 gives air-density difference (Dr – Dw) at the same conditions; this is to aid calculations with Equation 1. Values are given at 2°F intervals; intermediate values of temperature can be obtained by linear interpolation, as can intermediate values of relative humidity.
Sample Calculation
Consider the example of a swimming pool that is 100 ft long and 20 ft wide. Water temperature is maintained at 78°F. Building air is maintained at 80°F and 60 percent relative humidity. If there are 50 bathers:
N = 50
A = 100 × 20 = 2,000 sq ft
N ÷ A = 50 ÷ 2,000 = 0.025 people per square foot
From Table 2:
Dr – Dw = 0.0006 lb per cubic foot
From Table 1:
E0 = 0.0133 lb per hour per square foot
Using Equation 1:
E ÷ E0 = 1.9 – (336 × 0.0006) + (57 × 0.025) = 3.12
E = 3.12 × 0.0133 = 0.0415 lb per hour per square foot
Total evaporation = 2,000 × 0.0415 = 83 lb per hour
Trends of Various Formulas
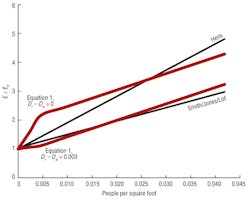
Figure 1 shows results obtained with the Smith/Jones/Lof and Hens formulas. According to those formulas, air-density difference (Dr – Dw) does not affect evaporation (E ÷ E0). Also shown are results for air-density differences of 0 and 0.003 lb per cubic foot obtained with Equation 1. At an air-density difference of 0 lb per cubic foot, the predictions of Equation 1 are fairly close to those of Hens. At an air-density difference of 0.003 lb per cubic foot, the predictions of Equation 1 are rather close to those of Smith, Jones, and Lof. The greater the air-density difference, the lesser the evaporation enhancement. Higher density differences occur when water temperature is higher than air temperature. Water spilling on a pool deck quickly cools to air temperature; therefore, evaporation per square foot is much less from a pool deck than it is from the pool's surface. If pool temperature and air temperature are nearly equal, however, water on the deck evaporates at the same rate as water from the pool's surface, and there is a large increase in total evaporation rate.
Comparison With Test Data
While many tests of occupied pools have been reported, analyzable data have been provided for only four: Doering,8 Hanssen and Mathisen,9 Heimann and Rink,10 and Biasin and Krumme.10 The data, which cover pools of 700 to 4,600 sq ft, a wide range of air and water conditions, and occupancies from 0.001 to 0.045 people per square foot (22 to 1,000 sq ft per person), were compared with results from calculations performed with the new method and six other formulas (Table 3). Results obtained with the new method were in good agreement with the data: 87 percent of the results were within ±30 percent of the data; the mean deviation for all data was 18.1 percent. The performance of the other formulas was much inferior, with only the Shah formulas5 in somewhat reasonable agreement with the data.
Summary and Conclusion
A new correlation for the effect of occupancy on the rate of evaporation from swimming pools was presented. It shows good agreement with available test data, the mean absolute deviation being 18 percent.
An important feature of the new correlation is that, in addition to number of occupants, it takes into account the effect of density difference between room air and air at a pool's surface. Earlier correlations do not consider the effect of density difference.
Several other published correlations were evaluated against the same data. Their performance was far inferior, with mean absolute deviation varying from 25 to 70 percent.
The new correlation will aid sizing of HVAC systems and estimates of swimming-pool energy use.
References
1) ASHRAE. (2011). ASHRAE handbook—HVAC applications. Atlanta: American Society of Heating, Refrigerating and Air-Conditioning Engineers.
2) VDI. (1994). Wärme, raumlufttechnik, wasserer- und –entsorgung in hallen und freibädern. VDI 2089.
3) Smith, C.C., Jones, R.W., & Lof, G.O.G. (1993). Energy requirements and potential savings for heated indoor swimming pools. ASHRAE Transactions, 99 (2), 864-874.
4) Hens, H. (2009). Indoor climate and building envelope performance in indoor swimming pools. Energy Efficiency and New Approaches, proceedings of the 4th International Building Physics Conference, pp. 543-552.
5) Shah, M.M. (2003). Prediction of evaporation from occupied indoor swimming pools. Energy & Buildings, 35, 707-713.
7) Shah, M.M. (2012). Calculation of evaporation from indoor swimming pools: Further development of formulas. ASHRAE Transactions, 118 (2).
8) Doering, E. (1979). Zur auslegung von luftungsanlagen fur Hallenschwimmbaeder. HLH, 30, 211-216.
9) Hanssen, S.A., & Mathisen, H.M. (1990). Evaporation from swimming pools. Paper presented at Roomvent 90: 2nd International Conference in Oslo, Norway.
10) Biasin, K., & Krumme, W. (1974). Die wasserverdunstung in einem innenschwimmbad. Electrowaerme International, 32 (A3), A115-A129.
Mirza M. Shah, PhD, PE, FASHRAE, FASME, long has been active in design, analysis, and research in the areas of HVAC, refrigeration, energy systems, and heat transfer. His formulas for boiling and condensation heat transfer are widely used and included in many engineering reference books. He can be contacted at [email protected]. For more information, visit www.mmshah.org.
This file type includes high resolution graphics and schematics when applicable.
Did you find this article useful? Send comments and suggestions to Executive Editor Scott Arnold at [email protected].